II Analysis of color separation algorithm based on concentration space
â–²1. Principle of electronic separation of black and white originals
Electronic color separation is based on the concentration space. This is essentially different from the separation of photoshop. It can also be said that the color separation of the electronic color separation machine is a device-dependent color separation, and the color separation of photoshop is based on the color space, and the color separation is independent of the device.
There is no separation of black-and-white manuscripts. There is only screening, that is, a continuous black-and-white manuscript is converted into a halftone screen print, and halftoning is used to express continuity.
Each point on the original is continuously scanned with a scanner, and the percentage of its screening is calculated based on the density of each dot. The scanner is essentially a black and white concentration meter.
The Murray_Davis formula for the percentage of dots and the tone density is derived below (see Figure 2)
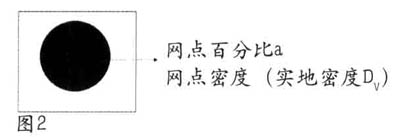
If the percentage of the network is α, then the percentage of the blank is 1-α. The dot density (equal to the full plate density) is set to DV, and the blank (paper) is set to O. Then, the total reflectance of the incident light to the incident light (set the incident light to 1) is 1i=α×1O.DV+(1-α)×1OO=1-α×(1-1O-DV). The tone density (dot dot area concentration) can be expressed as follows: D1 = lg1/[1-α×(1-1O.DV)]. Based on this, α=(1-1O.D1)/(1-1O.DV) can be introduced. The DV therein can be measured by measuring the printed full-plate concentration, thereby knowing the relationship between the tone density and the dot percentage. The scanner measures the density of each dot on the original (called the tone density after printing) to calculate the percentage of dots with this formula.
â–²2. Principle of color separation and screening of color originals
The scanning of the color manuscript shall collect the red, green and blue signals of each point separately. The principle is equivalent to a color concentration meter, that is, the three-color separation densities D1, Dg and Db can be measured separately for each point. To restore the original correctly, the percentage of the respective outlets of the yellow, magenta, and cyan versions is required (there is only a three-color version to restore the original).
If ink is the ideal ink, yellow ink absorbs only blue light and reflects all red and green light. Magenta ink absorbs only green light and reflects all red and blue light. Cyan ink absorbs only red light and reflects all green light. Blu-ray, the problem is very simple. For example, if it is determined that the color separation concentration D1 is the color separation concentration of red light, if D1 is to be restored, it is irrelevant to the percentage of the halftone dots and the percentage of the halftone dots of the product, because both of the two color plates will reflect red. Light (same as white paper), so it is only related to the percentage of cyan spots. The higher the percentage of cyan dots is, the more red light is absorbed and the larger is D1. Therefore, it is possible to measure the full plate density of the cyan plate, Drs (the greater the concentration value measured by the red filter, also called the color density or full plate density), and substituting the above Murray_Davis formula, so that the D1 and the cyan plate can be found. The relationship between the percentage of outlets.
It can be seen that the color separation of the ideal ink is actually using the Murray_Davis formula for the reflection concentration of each color light.
The actual ink is not the case. For example, although the yellow ink absorbs most of the blue light, it does not reflect all the red and green light. The same situation exists for the other two inks. We can actually measure the three-color separation concentration of three inks with a color densitometer, which is the measurement result of some ink (Table 1).

Therefore, the actual color separation must consider the factors of ink color deviation. For example, only the cyan ink is printed on the paper, and the solid printing is the 100% dot. It will produce a dichroic concentration of 1.50 for D1, ie, red light, and a green color separation concentration of 0.50 and a blue color separation concentration of 0.10. We set up the following formula, that is, the proportion coefficient of the color separation density of each color light is not changed. For example, if D1 of a dot percentage of blue dots is half of the original 0.75, the Dg and Db are also reduced by half. 0.25 and 0.05. This can be calculated separately as the ratio coefficient K5 is 0.50/1.50=0.33, K6=0.10/1.50=0.06. The other two inks are also calculated separately and the proportionality coefficient is listed in the above table.
Let the three concentrations at one point on the manuscript be Dro, Dgo, and Dbo, respectively. Then, the corresponding tone density (referred to as the tone density corresponding to the color density or full plate density) Dr, Dg, and Db is calculated for each ink after printing. The percentage of the respective dots can be obtained by substituting the obtained tone density into the Murray_Davis formula.
According to the principle of density superposition, the following equation can be listed:
Dro=K1×Db +K3×Dg+Dr
Dgo=K2×Db+Dg+K5×Dr
Dbo=Db+K4×Dg+K6×Dr
The above equation is a system of equations containing three unknowns Dr, Dg, Db. In the general case, the equation will have a unique solution. Substituting the solved Dr, Dg, and Db into the Murray_Davis formula, the percentage of dots for each color version can be found.
In some cases, the equation will have no solution. This is because the color gamut of the dot manuscript exceeds the gamut range that can be represented by the three-color ink superposition. In this case only the closest solution can be found.
The actual printing is to be added to the black version, and after the black version is added, the color gamut is expanded. The original solution that may not have been solved may become a solution. After the black version is added, the equation becomes three equations and four unknowns. There will be cases where there are no solutions. This means that the points on the original are not very saturated. The combinations of yellow, magenta, cyan, and black may or may not restore the color. . Generally, in this case, to determine the number of black editions, it is possible to determine the black edition first by UCR (Background Removal) or GCR (Uncolored Structure), and then calculate the number of other three kinds of editions.
(to be continued)